Answer:
0.000773 is the probability that atleast 12 out of 14 will have brown eyes.
Explanation:
We are given the following information:
We treat people having brown eyes as a success.
P(people have brown eyes) = 41% = 0.41
Then the number of people follows a binomial distribution, where
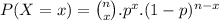
where n is the total number of observations, x is the number of success, p is the probability of success.
Now, we are given n = 14
We have to evaluate:
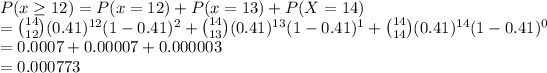
0.000773 is the probability that atleast 12 out of 14 will have brown eyes.
Yes, it is an unusual event due to small probability values.