Question

A particle in the first quadrant is moving along a path described by the equation LaTeX: x^2+xy+2y^2=16x 2 + x y + 2 y 2 = 16 such that at the moment its x-coordinate is 2, its y-coordinate is decreasing at a rate of 10 cm/sec. At what rate is its x-coordinate changing at that time?

Answer 1

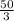`(50)/(3)` cm/sec.

Explanation:

We have been given that a particle in the first quadrant is moving along a path described by the equation
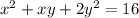`x^2+xy+2y^2=16` such that at the moment its x-coordinate is 2, its y-coordinate is decreasing at a rate of 10 cm/sec. We are asked to find the rate at which x-coordinate is changing at that time.

First of all, we will find the y value, when
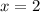`x =2` by substituting
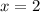`x =2` in our given equation.

`2^2+2y+2y^2=16`

`4-16+2y+2y^2=16-16`

`2y^2+2y-12=0`

`y^2+y-6=0`

`y^2+3y-2y-6=0`

`(y+3)(y-2)=0`

`(y+3)=0,(y-2)=0`

`y=-3,y=2`

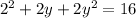
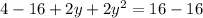
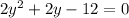
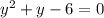
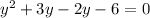
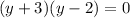
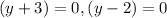
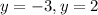
Since the particle is moving in the 1st quadrant, so the value of y will be positive that is
`y=2`.

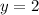Now, we will find the derivative of our given equation.

`2x\cdot x'+x'y+xy'+4y\cdot y'=0`

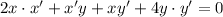
We have been given that
`y=2`,
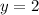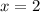`x =2` and
`y'=-10`.

`2(2)\cdot x'+(2)x'+2(-10)+4(2)\cdot (-10)=0`

`4\cdot x'+2x'-20-80=0`

`6x'-100=0`

`6x'-100+100=0+100`

`6x'=100`

`(6x')/(6)=(100)/(6)`

`x'=(50)/(3)`

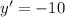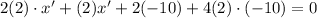
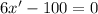
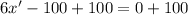
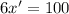
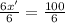
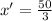
Therefore, the x-coordinate is increasing at a rate of
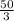`(50)/(3)` cm/sec.