Answer:
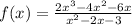
Explanation:
Roots of a denominator in a rational function gives to us the vertical asymptotes. Hence we can take the denominator as

if we want that the end behavior as y=2x we can choose a polynomial whose factors cancel out with the denominator. Thus
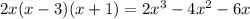
Hence, the function is
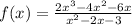
Hope this helps!!