Question

​It's believed that as many as 24​% of adults over 50 never graduated from high school. We wish to see if this percentage is the same among the 25 to 30 age group. What sample size would allow us to increase our confidence level to​ 95% while reducing the margin of error to only 4​%?

Answer 1

n=438

Explanation:

-Given the sample proportion
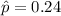`\hat p=0.24` and the confidence level is 95%.

-The sample size can be calculated using the formula;

`ME=z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

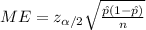
#Substitute parameters in the formula and make n the subject of the formula;

`ME=z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}\\\\=z_(0.025)\sqrt{(\hat p(1-\hat p))/(n)}\\\\n=((z_(0.025))/(ME))^2\hat p(1-\hat p)\\\\\\=((1.96)/(0.04))^2* 0.24* 0.76\\\\=437.94\approx 438`

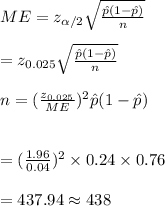
Hence, the desired sample size is n=438