Answer:
The probability of the student will pass the quiz = .0546
Explanation:
Given -
Total no of question = 10
If the student guesses on each question there are two outcomes true of false
the probability of guesses question correctly =

the probability of success is (p) =

the probability of guesses question incorrectly =

the probability of failure is (q) = 1- p =

If the student guesses on each question he must answered at least 8 question correctly
the probability of the student will pass the quiz =
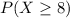
= P(X = 8 ) + P(X = 9) + P(X = 10 )
=
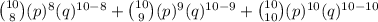
=
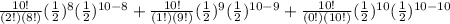
=
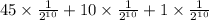
=
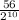
= .0546