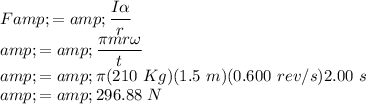Answer:
The value of the constant force is
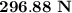 .
.
Step-by-step explanation:
Given:
Mass of the merry-go-round,

Radius of the horizontal disk,
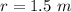
Time required,
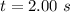
Angular speed,
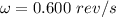
Torque on an object is given by

where
 is the moment of inertia of the object,
is the moment of inertia of the object,
 is the angular acceleration and
is the angular acceleration and
 is the force on the disk.
is the force on the disk.
The moment of inertia of the horizontal disk is given by

and the angular acceleration is given by
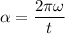
Substituting all these values in equation (1), we have