Answer:
3 ft by 4/3 feet.
Explanation:
We have been given that a card is 9 inches by 4 inches. A printing shop will enlarge it so that the longer side is any lengths up to 3 ft. We are asked to find the dimensions of biggest enlargement.
We will use proportions to solve our given problem.

Upon substituting our given values, we will get:
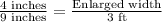
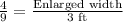
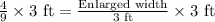
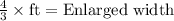
Therefore, the dimensions of the biggest enlargement would be 3 ft by 4/3 feet.