Question

Find the tangent plane to the given surface of f(x,y)=6- 6/5 x-y at the point (5, -1, 1). Make sure tat your final answer for the plane is in simplified form.

Answer 1

Required equation of tangent plane is
`z=(6)/(5)(x-5y-11)`.

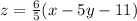Explanation:

Given surface function is,

`f(x,y)=6-(6)/(5)(x-y)`

To find tangent plane at the point (5,-1,1).

We know equation of tangent plane at the point $(x_0,y_0,z_0)[/tex] is,

`z=f(x_0,y_0)+f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)\hfill (1)`

So that,

`f(x_0,y_0)=6-(6)/(5)(5+1)=-(6)/(5)`

`f_x=-(6)/(5)y\implies f_x(5,-1,1)=(6)/(5)`

`f_y=-(6)/(5)x\implies f_y(5,-1,1)=-6`

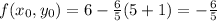
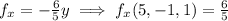
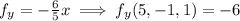
Substitute all these values in (1) we get,

`z=(6)/(5)(x-5)-6(y+1)-(6)/(5)`

`\therefore z=(6)/(5)(x-5y-11)`

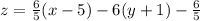
Which is the required euation of tangent plane.