Question

A brave child decides to grab onto an already spinning merry‑go‑round. The child is initially at rest and has a mass of 31.5 kg. The child grabs and clings to a bar that is 1.25 m from the center of the merry‑go‑round, causing the angular velocity of the merry‑go‑round to abruptly drop from 51.0 rpm to 17.0 rpm . What is the moment of inertia of the merry‑go‑round with respect to its central axis?

Answer 1

24.609375 kgm²

Step-by-step explanation:

I = Moment of inertia of the merry go round

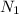`N_1` = Initial speed = 51 rpm

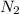`N_2` = Final speed = 17 rpm

m = Mass of child = 31.5 kg

r = Radius = 1.25 m

In this system the angular momentum is conserved

`IN_1=(I+mr^2)N_2\\\Rightarrow I* 51=(I+31.5* 1.25^2)17\\\Rightarrow I(51)/(17)-I=31.5* 1.25^2\\\Rightarrow 2I=49.21875\\\Rightarrow I=(49.21875)/(2)\\\Rightarrow I=24.609375\ kgm^2`

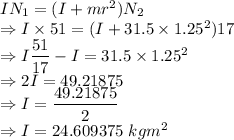
The moment of inertia of the merry go round is 24.609375 kgm²