Question

Compute the mean and standard deviation of the sampling distribution of the sample mean when you plan to take an SRS of size 49 from a population with mean 420 and standard deviation 21. Now repeat the calculations for a sample size of 576. Explain the effect of the increase on the sample mean and standard deviation.

Answer 1

The mean of the sampling distribution(SRS 49) of the sample mean is 420 and the standard deviation is 3.

The mean of the sampling distribution(SRS 576) of the sample mean is 420 and the standard deviation is 0.875.

By the Central Limit Theorem, the sample size does not influence the sample mean, but it does decrease the standard deviation of the sample

Explanation:

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

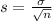For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

Population

mean = 420, standard deviation = 21.

Sample of 49

Mean = 420, standard deviation
`s = (21)/(√(49)) = 3`

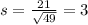
The mean of the sampling distribution of the sample mean is 420 and the standard deviation is 3.

Sample of 49

Mean = 420, standard deviation
`s = (21)/(√(576)) = 0.875`

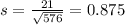
The mean of the sampling distribution of the sample mean is 420 and the standard deviation is 0.875.