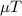Question

A very long, straight solenoid with a diameter of 3.00 cm is wound with 40 turns of wire per centimeter, and the windings carry a current of 0.240 A. A second coil having N turns and a larger diameter is slipped over the solenoid so that the two are coaxial. The current in the solenoid is ramped down to zero over a period of 0.70 s. What average emf is induced in the second coil if it has a diameter of 3.90 cm and N = 48? Express your answer in microvolts to two significant figures.What is the induced emf if the diameter is 7.80 cm and N = 96? Express your answer in volts to two significant figures.

Answer 1

Induced emf in first coil is 0.986
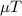`\mu T` and in second case 0.396
`\mu T`

Step-by-step explanation:

Given:

Number of turns per centimeter
`n = 40`

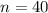
Current
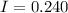`I = 0.240` A

Current rate
`(dI)/(dt) = (0.240)/(0.70) = 0.343`
`(A)/(s)`

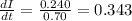
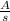
The magnetic field in solenoid is given by,

`B = \mu _(o) nI`

Where
`\mu _(o) = 4\pi * 10^(-7)`

We write,

`(dB)/(dt) = \mu_(o) n (dI)/(dt)`

`(dB)/(dt) = 4\pi * 10^(-7) * 40 * 0.343`

`(dB)/(dt) = 172.3 * 10^(-7)`

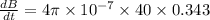
(A)

Number of turns
`N = 48`

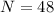
Radius of coil
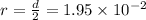`r = (d)/(2) = 1.95 * 10^(-2)` m

From faraday's law

`\epsilon = NA (dB)/(dt)`

Where
`A = \pi r^(2) = 3.14 (1.95 * 10^(-2) ) ^(2) = 11.93 * 10^(-4)`
`m^(2)`

`\epsilon = 48 * 11.93 * 10^(-4) * 172.3 * 10^(-7)`

`\epsilon = 98665.87 * 10^(-11)`

`\epsilon = 0.986 \mu T`

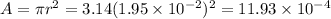
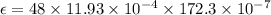
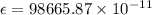
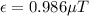
(B)

Number of turns
`N = 96`

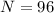
Radius of coil
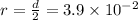`r = (d)/(2) = 3.9 * 10^(-2)` m

From faraday's law

`\epsilon = NA (dB)/(dt)`

Where
`A = \pi r^(2) = 3.14 (3.9 * 10^(-2) ) ^(2) = 47.76 * 10^(-4)`
`m^(2)`

`\epsilon = 48 * 47.96 * 10^(-4) * 172.3 * 10^(-7)`

`\epsilon = 396648.38 * 10^(-11)`

`\epsilon = 0.396 \mu T`

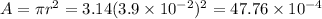
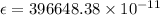
Therefore, induced emf in first coil is 0.986
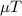`\mu T` and in second case 0.396
`\mu T`