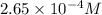This is an incomplete question, here is a complete question.
The concentration of Cu²⁺ ions in the water (which also contains sulfate ions) discharged from a certain industrial plant is determined by adding excess sodium sulfide (Na₂S)solution to 0.700 L of the water.
The molecular equation is:

Write the net ionic equation and calculate the molar concentration of Cu²⁺ in the water sample if 0.0177 g of solid CuS is formed.
Answer :
The net ionic equation will be,
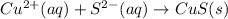
The concentration of
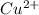 is,
is,
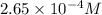
Explanation :
In the net ionic equations, we are not include the spectator ions in the equations.
Spectator ions : The ions present on reactant and product side which do not participate in a reactions. The same ions present on both the sides.
The molecular equation is:

The ionic equation in separated aqueous solution will be,
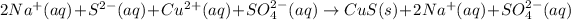
In this equation,
 are the spectator ions.
are the spectator ions.
By removing the spectator ions from the balanced ionic equation, we get the net ionic equation.
The net ionic equation will be,
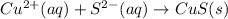
Now we have to calculate the mass of
Molar mass of
 = 159.5 g/mol
= 159.5 g/mol
Molar mass of CuS is = 95.5 g/mol
From the balanced chemical reaction we conclude that,
As, 95.5 g of CuS produces from 159.5 g
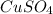
As, 0.0177 g of CuS produces from
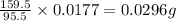
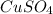
Now we have to calculate the concentration of
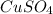
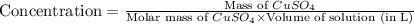
Now put all the given values in this formula, we get:
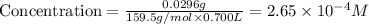
Concentration of
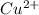 =
=
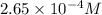
Therefore, the concentration of
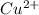 is,
is,