Question

A 0.450-kg hockey puck, moving east with a speed of 5.25 m/s , has a head-on collision with a 0.850-kg puck initially at rest. Assuming a perfectly elastic collision, what will be the speed (magnitude of the velocity) of each object after the collision

Answer 1

Step-by-step explanation:

Given that,

Mass of the hockey puck, m₁ = 0.45 kg

Initial peed of the hockey puck, u₁ = 5.25 m/s (east)

Mass of other puck, m₁ = 0.85 kg

Initial speed of other puck, u₂ = 0 (at rest)

Let v₁ and v₂ are the final speeds of both pucks after the collision respectively. Using the conservation of momentum as :

`m_1u_1+m_2u_2=m_1v_1+m_2v_2\\\\m_1v_1+m_2v_2=0.45* 5.25+0.85* 0\\\\m_1v_1+m_2v_2=2.36\\\\0.45v_1+0.85v_2=2.36.........(1)`

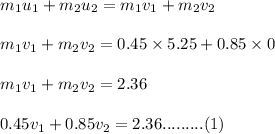
The coefficient of restitution for elastic collision is equal to 1.

`C=(v_2-v_1)/(u_1-u_2)\\\\1=(v_2-v_1)/(u_1-u_2)\\\\1=(v_2-v_1)/(5.25-0)\\\\v_2-v_1=5.25.......(2)`

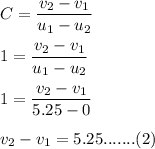
On solving equation (1) and (2) we get :

`v_1=-1.611\ m/s\\\\v_2=3.63 m/s`

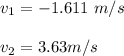
Hence, this is the required solution.