Question

In a large lecture class, the professor announced that the scores on a recent exam were normally distributed with a range from 51 to 87. Using the Empirical Rule μ ± 3σ to estimate σ, how many students would you need to sample to estimate the true mean score for the class with 90 percent confidence and an error of ±2?

Answer 1

The standard deviation of the scores on a recent exam is 6.

The sample size required is 25.

Explanation:

Let X = scores of students on a recent exam.

It is provided that the random variable X is normally distributed.

According to the Empirical rule, 99.7% of the normal distribution is contained in the range, μ ± 3σ.

That is, P (μ - 3σ < X < μ + 3σ) = 0.997.

It is provided that the scores on a recent exam were normally distributed with a range from 51 to 87.

This implies that:

P (51 < X < 87) = 0.997

So,

μ - 3σ = 51...(i)

μ + 3σ = 87...(ii)

Subtract (i) and (ii) to compute the value of σ as follows:

μ - 3σ = 51

(-)μ + (-)3σ = (-)87

______________

-6σ = -36

σ = 6

Thus, the standard deviation of the scores on a recent exam is 6.

The (1 - α)% confidence interval for population mean is given by:

`CI=\bar x\pm z_(\alpha/2)(\sigma)/(√(n))`

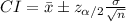
The margin of error of this interval is:

`MOE = z_(\alpha/2)(\sigma)/(√(n))`

Given:

MOE = 2

σ = 6

Confidence level = 90%

Compute the z-score for 90% confidence level as follows:

`z_(\alpha/2)=z_(0.10/2)=z_(0.05)=1.645`

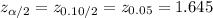
*Use a z-table.

Compute the sample required as follows:

`MOE = z_(\alpha/2)(\sigma)/(√(n))\\2=1.645* (6)/(√(n))\\n=((1.645* 6)/(2))^(2)\\n=24.354225\\n\approx 25`

Thus, the sample size required is 25.