Answer:
a) Expected value = 6.406
Variance = 4.905
Standard deviation = 2.45
b) The probability is 0.08547
Explanation:
a) Let's suppose that:
X₁ = number of 6´s
X₂ = number of Jack, Queen, King or Aces
The mean of X₁ is:
MeanX₁ = n * p = 20 * (1/6) = 3.33
The variance of X₁ is:

The mean of X₂ is:
MeanX₂ = 10 * (16/52) = 3.076
The variance of X₂ is:
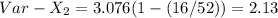
The expect value of X is:
Xexp = MeanX₁ + MeanX₂ = 3.33 + 3.076 = 6.406
The variance of X is:
VarX = VarX₁ + VarX₂ = 2.775 + 2.13 = 4.905
The standard deviation is:
Xdevi = 4.905/2 = 2.45
b) The probability of drawing at least five six out of 20 rolls is equal to:
∑(1/6)ˣ(5/6)²⁰⁻ˣ = 0.231 with x = 5
The probability of at least 4 Jack, Queen, Kings or Aces is:
∑(16/52)ˣ(1-(16/52))¹⁰⁻ˣ = 0.37 with x = 4
The probability of given event is equal to:
P = 0.231 * 0.37 = 0.08547