Answer:
a)Null hypothesis:- H₀: μ> 500
Alternative hypothesis:-H₁ : μ< 500
b) (5211.05 , 5411.7)
95% lower confidence bound on the mean.
c) The test of hypothesis t = 5.826 >1.761 From 't' distribution table at 14 degrees of freedom at 95% level of significance.
Explanation:
Step :-1
Given a random sample of 15 devices is selected in the laboratory.
size of the small sample 'n' = 15
An average life of 5311.4 hours and a sample standard deviation of 220.7 hours.
Average of sample mean (x⁻) = 5311.4 hours
sample standard deviation (S) = 220.7 hours.
Step :- 2
a) Null hypothesis:- H₀: μ> 500
Alternative hypothesis:-H₁ : μ< 500
Level of significance :- α = 0.95 or 0.05
b) The test statistic


t = 5.826
The degrees of freedom γ= n-1 = 15-1 =14
tabulated value t =1.761 From 't' distribution table at 14 degrees of freedom at 95% level of significance.
calculated value t = 5.826 >1.761 From 't' distribution table at 14 degrees of freedom at 95% level of significance.
Null hypothesis is rejected at 95% confidence on the mean.
C) The 95% of confidence limits
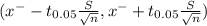
substitute values and simplification , we get
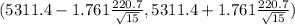
(5211.05 , 5411.7)
95% lower confidence bound on the mean.