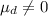Answer:
x=test value before , y = test value after
The system of hypothesis for this case are:
Null hypothesis:
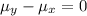
Alternative hypothesis:

If we define the difference as
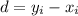 we convert the system of hypothesis:
we convert the system of hypothesis:
Null hypothesis:
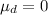
Alternative hypothesis:
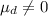
Explanation:
Previous concepts
A paired t-test is used to compare two population means where you have two samples in which observations in one sample can be paired with observations in the other sample. For example if we have Before-and-after observations (This problem) we can use it.
Let put some notation
x=test value before , y = test value after
The system of hypothesis for this case are:
Null hypothesis:
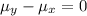
Alternative hypothesis:

If we define the difference as
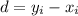 we convert the system of hypothesis:
we convert the system of hypothesis:
Null hypothesis:
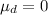
Alternative hypothesis: