Answer:
The Cohen's D is given by this formula:
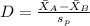
Where
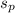 represent the deviation pooled and we know from the problem that:
represent the deviation pooled and we know from the problem that:
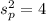 represent the pooled variance
represent the pooled variance
So then the pooled deviation would be:
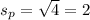
And the difference of the two samples is
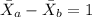 , and replacing we got:
, and replacing we got:
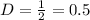
And since the value for D obtained is 0.5 we can consider this as a medium effect.
Explanation:
Previous concepts
Cohen’s D is a an statistical measure in order to analyze effect size for a given condition compared to other. For example can be used if we can check if one method A has a better effect than another method B in a specific situation.
Solution to the problem
The Cohen's D is given by this formula:
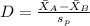
Where
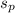 represent the deviation pooled and we know from the problem that:
represent the deviation pooled and we know from the problem that:
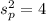 represent the pooled variance
represent the pooled variance
So then the pooled deviation would be:
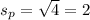
And the difference of the two samples is
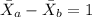 , and replacing we got:
, and replacing we got:
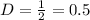
And since the value for D obtained is 0.5 we can consider this as a medium effect.