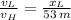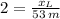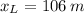Question

An object with mass 3M is launched straight up. When it reaches its maximum height, a small explosion breaks the object into two pieces with masses M and 2M. The explosion provides an impulse to each object in the horizontal direction only. The heavier of the two pieces is observed to land a distance 53 m from the point of the original launch. How far from the original launch position does the lighter piece land

Answer 1

`x_(L) = 106\,m`

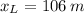
Step-by-step explanation:

Each piece is analyzed by using the Principle of Momentum Conservation and the Impulse Theorem:

Heavier object:

`(2\cdot M)\cdot (0) + F\cdot \Delta t = (2\cdot M)\cdot v_(H)`

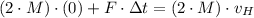
Lighter object:

`M\cdot (0) + F\cdot \Delta t = M\cdot v_(L)`

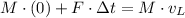
After the some algebraic handling, the following relationship is found:

`M\cdot v_(L) = 2\cdot M\cdot v_(H)`

`v_(L) = 2\cdot v_(H)`

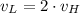
Given that both pieces have horizontal velocities only and both are modelled as projectiles, the horizontal component of velocity remains constant and directly proportional to travelled distance. Then:

`(v_(L))/(v_(H)) = (x_(L))/(53\,m)`

`2 = (x_(L))/(53\,m)`

`x_(L) = 106\,m`