Answer:
The probability that 10 or more of them used their phones for guidance on purchasing decisions =
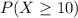 = .278
= .278
Explanation:
Given -
A study conducted by the Pew Research Center reported that 58% of cell phone owners used their phones inside a store for guidance on purchasing decisions .
Then the probability of success is (p) = 58
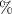 = .58
= .58
the probability of failure is (q) = 1 - p = .42
sample size n = 15
Let X be the no of owners used their phones for guidance on purchasing decisions
Using the formula
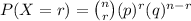
The probability that 10 or more of them used their phones for guidance on purchasing decisions =
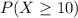
= P(X = 10) + P(X = 11) + P(X = 12) + P(X = 13) + P(X = 14) + P(X = 15)
=
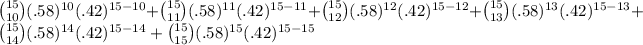 =
=
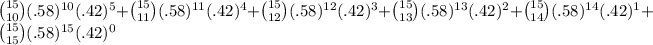
=
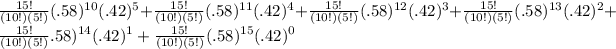 =
=
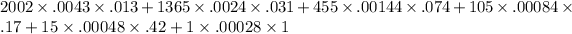
= .1119 + .1015 + .048 + .014 + .0030 + .00028
= .278