Question

The mass of a particular eagle is twice that of a hunted pigeon. Suppose the pigeon is flying north at v i , 2 = 17.3 vi,2=17.3 m/s when the eagle swoops down, grabs the pigeon, and flies off. At the instant right before the attack, the eagle is flying toward the pigeon at an angle θ = 39.9 θ=39.9 ° below the horizontal and a speed of v i , 1 = 33.7 vi,1=33.7 m/s. What is the speed of the eagle immediately after it catches its prey?

Answer 1

19.29 m/s

Step-by-step explanation:

Apply the conservation of linear momentum in north-south direction:

`m_pv_p+m_ev_e sin \theta = (m_p+m_e)v_f sin \phi\\m_p (17.3)+(2m_p)(33.7 sin (-39.9))=3m_p v_f sin \phi\\17.3-43.23=3v_fsin\phi\\\Rightarrow v_f sin\phi = -8.64`

Apply the conservation of linear momentum in east-west direction:

`m_ev_e cos \theta = (m_p+m_e)v_f cos \phi\\2m_p (33.7)cos (39.9) = 3 m_pv_f cos\phi\\\Rightarrow v_f cos\phi = 17.23`

Dividing the two equations:

`tan \phi = (-8.64)/(17.23) \\\phi = -26.6^o`

`v_f sin \phi = -8.64 \\v_f = (-8.64)/(sin (-26.6^o)) = 19.29 m/s`

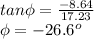
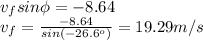
Thus, the speed of the eagle immediately after it catches its prey is 19.29 m/s.