Answer:
0.67% probability he will have to shut down after this month
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:
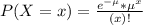
In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given time interval.
is the mean in the given time interval.
On average sells 8.9 machines per month.
So
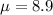
Using the Poisson distribution, what is the probability he will have to shut down after this month
If he sells less than 3 machines.
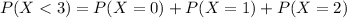
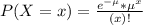
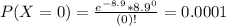
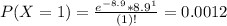
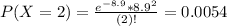
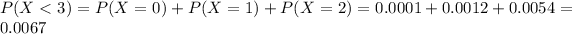
0.67% probability he will have to shut down after this month