Question

A travelling salesman sells milkshake mixing machines and on average sells 8.9 machines per month. He needs to sell at least 3 machines each month order to stay in business, otherwise he will shut down. Using the Poisson distribution, what is the probability he will have to shut down after this month

Answer 1

0.67% probability he will have to shut down after this month

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

On average sells 8.9 machines per month.

So
`\mu = 8.9`

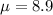
Using the Poisson distribution, what is the probability he will have to shut down after this month

If he sells less than 3 machines.

`P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)`

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-8.9)*8.9^(0))/((0)!) = 0.0001`

`P(X = 1) = (e^(-8.9)*8.9^(1))/((1)!) = 0.0012`

`P(X = 2) = (e^(-8.9)*8.9^(2))/((2)!) = 0.0054`

`P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.0001 + 0.0012 + 0.0054 = 0.0067`

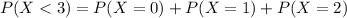
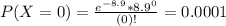
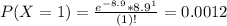
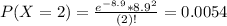
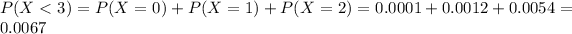
0.67% probability he will have to shut down after this month