Question

A 2.50 kg fireworks shell is fired straight up from a mortar and reaches a height of 110.0 m. a) Neglecting air resistance (a poor assumption, but we will make it for this example), calculate the shell’s velocity when it leaves the mortar. b) The mortar itself is a tube 0.450 m long. Calculate the average acceleration of the shell in the tube as it goes from zero to the velocity found in a). c) What is the average force on the shell in the mortar? Express your answer in newtons and as a ratio to the weight of the shell.

Answer 1

a) the initial velocity ot the firework shell is 46.5m/s

b) the average acceleration of the shell in the tube is 2.4 × 10³m/s²

c) the average force on the shell in the tube is 2.4 × 10³m/s²

the ratio of the average force acting on the shell to the weight of the shell is 244.65 : 1

Step-by-step explanation:

Given that;

Mass, m = 2.5 kg

Height, h = 110m

Length , L = 0.45m

The expression of the relationship between velocity and distance kinematic law of motion

`v^2 = u^2 - 2gh`

`u = √(v^2+2gh)`

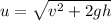
At maximum height the velocity of the firework shell is zero

That is why the final velocity of the firework shell is zero

`u = √(2gh)`

`u = √(2* 9.81 * 110) \\\\u = 46.5m/s`

Hence, the initial velocity ot the firework shell is 46.5m/s

b)

`v^2 = u^2 + 2as`

`a = (v^2 - u^2)/(2s)`

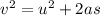
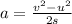
The initial velocity of the shell in the tube is zero

`a = (v^2)/(2s) \\`

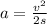
substitute 46.5m/s for v and 0.450 for s

`a = (46.5^2)/(2* 0.450) \\\\a = 2.4 * 10 ^3m/s^2`

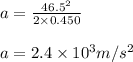
Hence , the average acceleration of the shell in the tube is 2.4 × 10³m/s²

c)

From Newton's law of motion,

Average Force, F = ma

substitute 2.50kg for m and 2.4 × 10³m/s² for a

F = ( 2.50kg )(2.4 × 10³m/s²)

F = 6 × 10³N

Hence, the average force on the shell in the tube is 2.4 × 10³m/s²

Calculate the weight of the shell

W = mg

substitute 2.50kg for m and 9.81m/s² for g

W = (2.50kg)( 9.81m/s²)

W = 24.525N

Calculate the ratio of the average force acting on the shell in the tube to the weight of the shell

`Ratio = (F)/(W)`

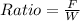
substitute 24.525N for W and 6 × 10³N for F

`Ratio = (6 * 10^3N)/(24.525N) \\\\= 244.65`

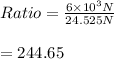
Hence , the ratio of the average force acting on the shell to the weight of the shell is 244.65 : 1

Answer 2

A) 46.43 m/s

B) Acceleration = 2395.27 m/s²

C) Average force in Newton's = 5988.18 N

Ratio of this force to weight = 244.14

Step-by-step explanation:

We are given that;

Mass; m = 2.5 kg

Height reached by firework; y = 110m

Length of tube;L = 0.45m

A) According to kinematic equation;

v² = u² + 2gs

In this case, v = 0 and because gravity is acting against motion. Thus,

0 = u² - 2gy

u² = 2gy

u = √2gy

Plugging in the relevant values ;

u = √(2 x 9.8 x 110)

u = √2156

u = 46.43 m/s

B) we want to find the acceleration with u = 0 m/s and v = 46.43 m/s in the tube. The tube length is 0.45m

Thus,

v² = u² + 2aL

46.43² = 0 + (2•a•0.45)

2155.7449 = 0.9a

acceleration, a = 2155.7449/0.9 = 2395.27 m/s²

C) From Newton's law of motion,

Average Force; F = ma

Thus, F = 2.5 x 2395.27 = 5988.18 N

We are told to express it as a ratio to the weight of the shell.

Thus, ratio = F/W

Weight = mg and force = ma

Thus, F/W = ma/mg = a/g = 2395.27/9.8 = 244.42