Question

g A window is being built and the bottom is a rectangle and the top is a semi-circle. If there is 12 meters of framing materials, what must the dimensions of the window be to let in the most light?

Answer 1

The problem is to maximize the area of a window consisting of a rectangle and a semi-circle on top, given a fixed perimeter of framing material, which is a high school level optimization problem in geometry and calculus.

Step-by-step explanation:

The question addresses the problem of finding the dimensions of a window with the most amount of light passing through, given a fixed amount of framing material. This is a classic problem in mathematics involving optimization under constraints, specifically related to geometry and calculus.

Let the width of the rectangle be x meters, and its height be y meters. Since the top of the window is a semi-circle, its diameter is equal to the width of the rectangle, meaning the radius of the semi-circle is x/2 meters. The perimeter of the entire window consists of the two sides and the bottom of the rectangle, and the circumference of the semi-circle. The total length of framing material is 12 meters, hence:

2y + x + (π(x/2)/2) = 12

Since the area of rectangle A = x*y and the area of the semi-circle is (x/2)²)/2, we want to maximize the total area A = x*y + (x/2)²)/2.

Using calculus, one can differentiate the area with respect to x or y and set the derivative equal to zero to find the maximum value. Assuming the student knows basic differentiation and solving equations, they can arrive at the optimal dimensions to let in the most light.

Answer 2

Semicircle of radius of 1.6803 meters

Rectangle of dimensions 3.3606m x 1.6803m

Step-by-step explanation:

Let the radius of the semicircle on the top=r

Let the height of the rectangle =h

Since the semicircle is on top of the window, the width of the rectangular portion =Diameter of the Semicircle =2r

The Perimeter of the Window

=Length of the three sides on the rectangular portion + circumference of the semicircle

`=h+h+2r+\pi r=2h+2r+\pi r=12`

The area of the window is what we want to maximize.

Area of the Window=Area of Rectangle+Area of Semicircle

`=2hr+(\pi r^2)/(2)`

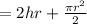
We are trying to Maximize A subject to
`2h+2r+\pi r=12`

`2h+2r+\pi r=12\\h=6-r-(\pi r)/(2)`

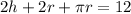
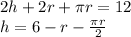
The first and second derivatives are,

Area, A(r)
`=2r(6-r-(\pi r)/(2))+(\pi r^2)/(2)}=12r-2r^2-(\pi r^2)/(2)`

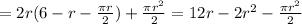
Taking the first and second derivatives

`A'\left( r \right) = 12 - r\left( {4 + \pi } \right)\\A''\left( r \right) = - 4 - \pi`

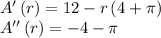
From the two derivatives above, we see that the only critical point of r

`A'\left( r \right) = 12 - r\left( {4 + \pi } \right)=0`

`r = \frac{{12}}{{4 + \pi }} = 1.6803`

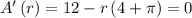
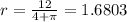
Since the second derivative is a negative constant, the maximum area must occur at this point.

`h=6-1.6803-(\pi X1.6803)/(2)=1.6803`

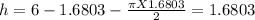
So, for the maximum area the semicircle on top must have a radius of 1.6803 meters and the rectangle must have the dimensions 3.3606m x 1.6803m ( Recall, The other dimension of the window = 2r)