Answer:
The density increases by 5 times
Step-by-step explanation:
We can solve this problem by using the equation of state of an ideal gas:
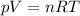
where
p is the pressure of the gas
V is its volume
n is its number of moles
R is the gas constant
T is the Kelvin temperature
Since n and R are constant during a gas transformation, we can rewrite the equation as

In thhis problem we have:
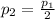 , since the pressure of the gas is cut in half
, since the pressure of the gas is cut in half
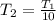 , since the gas temperature decreases by 10 times
, since the gas temperature decreases by 10 times
Therefore solving for V2, we find how much does the volume of the gas change:
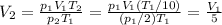
So, the volume decreases by 5 times.
The density of the gas is given by
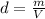
where m is the mass of the gas and V its volume. Here, the mass of the gas remains constant: so, the density is inversely proportional to the volume. Therefore, if the volume decreases by 5 times, the density will increase by 5 times.