Answer:
The dimensions are 32 ft by 16 ft
Explanation:
Area of the coffee and recreation room=512 square foot
LB=512
L=512/B
Perimeter of the Room = Perimeter of north wall+Perimeter of east wall+ Perimeter of west wall =L+2B (West and East are opposite)
Cost of the Perimeter=16L+4(2B)
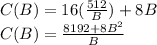
To minimize cost, first, we take the derivative of C(B)
Using quotient rule
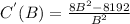
Setting the derivative equal to zero
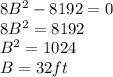
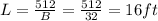
The dimension of the cheapest recreation area will be 32 ft by 16 ft