Question

A survey of athletes at a high school is conducted, and the following facts are discovered: 68% of the athletes are football players, 26% are basketball players, and 23% of the athletes play both football and basketball. An athlete is chosen at random from the high school: what is the probability that the athlete is either a football player or a basketball player

Answer 1

71%

Explanation:

Applying Venn's diagram

probabilty that an athlete plays either football or basketball

P ( A ∪ B ) = a + b + ( A ∩ B ) equation 1

note:

P ( A ) = a + ( A ∩ B )

( A ∩ B ) = 23% = 0.23

a = P( A ) - 0.23 = 0.68 - 0.23 = 0.45

P ( B ) = b + ( A ∩ B )

b = P ( B ) - ( A ∩ B ) = 0.26 - 0.23 = 0.03

back to equation 1

P ( A ∪ B ) = 0.45 + 0.03 +( 0.23 )

= 0.48 + ( 0.23 ) = 0.71 = 71%

P( A ) = probability of football players

P ( B ) = probability of basketball players

a = probability of playing football but not basketball

b = probabilty of playing basketball but not football

Answer 2

71% probability that the athlete is either a football player or a basketball player

Explanation:

We solve this problem building the Venn's diagram of these probabilities.

I am going to say that:

A is the probability that an athlete is a football player.

B is the probability that an athlete is a basketball players.

We have that:

`A = a + (A \cap B)`

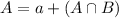
In which a is the probability that an athlete plays football but not basketball and
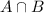`A \cap B` is the probability that an athlete plays both these sports.

By the same logic, we have that:

`B = b + (A \cap B)`

23% of the athletes play both football and basketball.

This means that
`A \cap B = 0.23`

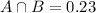
26% are basketball players

This means that
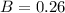`B = 0.26`. So

`B = b + (A \cap B)`

`0.26 = b + 0.23`

`b = 0.03`

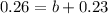
68% of the athletes are football players

This means that
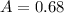`A = 0.68`. So

`A = a + (A \cap B)`

`0.68 = a + 0.23`

`a = 0.45`

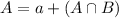
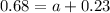
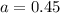
What is the probability that the athlete is either a football player or a basketball player

`A \cup B = a + b + (A \cap B)`

`A \cup B = 0.45 + 0.03 + 0.23 = 0.71`

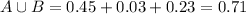
71% probability that the athlete is either a football player or a basketball player