Question

A motel finds it can rent 180 rooms when the room rate is $ 60 per day. For each $ 2 increase in the rate, two fewer rooms are rented. Find the room rate that maximizes daily revenue. The rate that maximizes revenue is $ .

Answer 1

The rate that maximizes revenue is $14,000

Explanation:

First of all, you should know that the income equation is:

R = p * n

where:

• p = price per item
• n = number of items sold

On the other hand, if p + x means a price increase, while n - x means a decrease in the number of an item sold.

In this case, reference is made to rooms, where 60 + 2x is the increased price and 180-2x is the decrease in rooms for rent.

So:

R=(60+2x)*(180-2x)

Expressing this in another way, applying distributive property:

R=60*180+60*(-2)x+2x*180+2x*(-2)x

R=10,800+240x-4x² equation (A)

This is a quadratic equation that is graphically represented by a parabola. If a, the coefficient that accompanies the term x², has a positive value, the parabola will be oriented upwards. On the contrary, if a has a negative value, the parabola will be oriented downwards. In this case, the value of a is -4, with the parabola facing down. The vertex is a point that is part of the parabola, which has the value as ordered minimum or maximum function. In this case, since the parabola faces downward, the vertex will be its maximum value.

The value of x in the vertex is
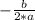`-(b)/(2*a)`. In this case:

• a=-4
• b=240

Replacing:

`x=-(240)/(2*(-4))`

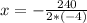
Solving:

x=40

To find the rate that maximizes income you simply replace this value in equation (A)

R=10,800+240*40-4*(40)²

R=14,000

The rate that maximizes revenue is $14,000

Answer 2

$7,200

Explanation:

r=p × n

where

r=revenue

p = price per item

n = number of items sold

A change in price changes quantity ( number sold)

Variable x changes with price, then

Let

p+x=a dollar price increase

p-x= a dollar price decrease

n+x= an increase in quantity sold

n-x= a decrease in quantity sold

Therefore,

A $2 dollar increase in price=p+2x

2 decrease in room quantity sold= n-2x

Substituting in the above equation

r=(p+2x)*(n-2x)

P=$60

n=180

Then

r=(60+2x)*(180-2x)

r=10,800-120x+360x-4x^2

r=-4x^2-240x+10,800

Solve the quadratic equation

The maximum value of x in the vertex = - b/2*a

Where

b=240

a=-4

Value of x=-240/2*(-4)

X=30

r=-4x^2-240x+10,800

=-4(30)^2-240(30)+10,800

=-4(900)-7200+10,800

=3,600-7200+10800

=$7,200

The rate that maximises revenue=$7,200