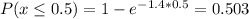Answer:
The probability is 0.503
Explanation:
If the ghost appearances occur in the house according to a Poisson process with mean m, the time between appearances follows a exponential distribution with mean 1/m. so, the probability that the next ghost appearance happens before x hours is equal to:
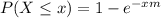
Then, replacing m by 1.4 ghosts per hour we get:
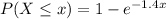
Additionally, The exponential distribution have a memoryless property, so if it is now 1:00 p.m. and we want the probability that ghost appear before 1:30 p.m., we need to find the difference in hours from 1:00 p.m and 1:30 p.m. no matter that the last ghost appearance was at 12:35 p.m.
Therefore, there are 0.5 hours between 1:00 p.m. and 1:30 p.m, so the probability that the 7th ghost will appear before 1:30 p.m is calculated as: