Question

At a given instant an object has an angular velocity. It also has an angular acceleration due to torques that are present. Therefore, the angular velocity is changing. Does the angular velocity at this instant increase, decrease, or remain the same (a) if additional torques are applied so as to make the net torque suddenly equal to zero and (b) if all the torques are suddenly removed

Answer 1

a) Constant

b) Constant

Step-by-step explanation:

a)

We can answer this question by using the equivalent of Newton's second law of motion of rotational motion, which can be written as:

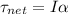`\tau_(net) = I \alpha` (1)

where

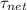`\tau_(net)` is the net torque acting on the object in rotation

I is the moment of inertia of the object

`\alpha` is the angular acceleration

The angular acceleration is the rate of change of the angular velocity, so it can be written as

`\alpha = (\Delta \omega)/(\Delta t)`

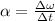
where

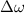`\Delta \omega` is the change in angular velocity

`\Delta t` is the time interval

So we can rewrite eq.(1) as

`\tau_(net)=I(\Delta \omega)/(\Delta t)`

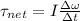
In this problem, we are told that at a given instant, the object has an angular acceleration due to the presence of torques, so there is a non-zero change in angular velocity.

Then, additional torques are applied, so that the net torque suddenly equal to zero, so:

`\tau_(net)=0`

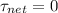
From the previous equation, this implies that

`\Delta \omega =0`

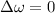
Which means that the angular velocity at that instant does not change anymore.

b)

In this second case instead, all the torques are suddenly removed.

This also means that the net torque becomes zero as well:

`\tau_(net)=0`

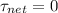
Therefore, this means that

`\Delta \omega =0`

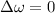
So also in this case, there is no change in angular velocity: this means that the angular velocity of the object will remain constant.

So cases (a) and (b) are basically the same situation, as the net torque is zero in both cases, so the object acts in the same way.