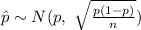Answer:
The distribution of sample proportion Americans who can order a meal in a foreign language is,
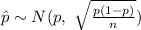
Explanation:
According to the Central limit theorem, if from an unknown population large samples of sizes n > 30, are selected and the sample proportion for each sample is computed then the sampling distribution of sample proportion follows a Normal distribution.
The mean of this sampling distribution of sample proportion is:
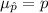
The standard deviation of this sampling distribution of sample proportion is:
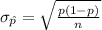
The sample size of Americans selected to disclose whether they can order a meal in a foreign language is, n = 200.
The sample selected is quite large.
The Central limit theorem can be applied to approximate the distribution of sample proportion.
The distribution of sample proportion is,