Question

A dielectric cube of side a, centered at the origin, carries a "frozen-in" polarization P = kr, where k is a constant. Find all the bound charges and check that they add up to zero.

Answer 1

The total volume of bound charge is zero.

Step-by-step explanation:

We have to the volume and surface bounded charge densities.

ρb = - Δ . p = - Δ .k (
`x^(X)` +
`y^(Y)` +
`x^(Y)`)

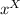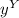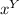= - 3k

On the top of the cube the surface charge density is

σb = p . z

=
`(ka)/(2)`

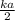
By symmetry this holds for all the other sides. The total bounded charge should be zero

Qtot = (-3k)a³ + 6 .
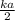`(ka)/(2)` . a² = 0

σb = -3K σb =
`(ka)/(2)`

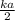
Qtot = 0

Hence, the total volume of bound charge is zero.