Question

A 12-foot ladder leans against the wall; the base of the ladder is 2 feet away from the wall.To the nearest tenth of a foot, how far up the wall does the ladder reach?

Answer 1

The ladder will reach a height of 11.8 feet up the wall

Solution:

The ladder, wall and base of the ladder from wall forms a right angled triangle

Length of ladder forms the hypotenuse

Length of ladder = 12 foot

base of the ladder from wall = 2 feet

To find: height of wall

By pythagoras theorem.

`c^2 = a^2+b^2`

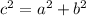
Where,

"c" is the Length of ladder

"a" is the base of the ladder from wall

"b" is the height of wall

Substituting the values,

`12^2 = 2^2+b^2\\\\144 = 4 + b^2\\\\b^2 = 140\\\\b = \pm 11.832 \\\\Ignore\ negative\ value\\\\b \approx 11.8`

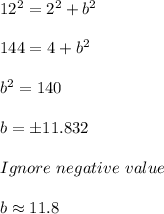
Thus, the ladder will reach a height of 11.8 feet on wall