Question

A clinical trial tests a method designed to increase the probability of conceiving a girl. In the study 425 babies were​ born, and 340 of them were girls. Use the sample data to construct a 99​% confidence interval estimate of the percentage of girls born. Based on the​ result, does the method appear to be​ effective? 0.75less than pless than 0.85 ​(Round to three decimal places as​ needed.) Does the method appear to be​ effective? No​, the proportion of girls is not significantly different from 0.5. Yes​, the proportion of girls is significantly different from 0.5.

Answer 1

0.75<p<0.85

Yes,the proportion of girls is significantly different from 0.5.

Explanation:

We calculate the proportion of girls:

`p=(340)/(425)\\\\\\\\=0.8`

#We then calculate the confidence interval as follows:

`CI=p\pm z(ME)\\\\=p\pm z_(0.005)\sqrt{(p(1-p))/(n)}\\\\=0.8+2.576* \sqrt{(0.8* 0.2)/(425)}\\\\=0.8\pm0.05\\\\=[0.75,0.85]`

Hence, the proportion's confidence interval at 99% is 0.75<p<0.85

#We then state our hypothesis to validate the claim:

`H_o:p=0.5\\H_a:p>0.5\\\\p=0.8(True \ mean)`

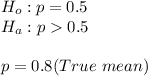
Since the confidence interval does not contain 0.5, which is the the 50% chance of having a girl, then it can be concluded the proportion of girls is significantly different from 0.5.