Given:
ABC is a right triangle and AC = BC
The length of AB is
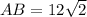
We need to determine the length of each of the legs.
Length of AC and BC:
Let the length of AC and BC be x.
The length of AC and BC can be determined using the Pythagorean theorem.
Thus, we have;
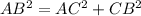
Substituting the values, we have;
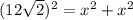
Simplifying, we get;
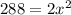
Dividing both sides by 2, we get;
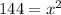
Taking square root on both sides, we get;
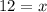
Thus, the length of each legs is 12 units.
Hence, the length of AC and BC are 12 units each.