Answer:
The mean waiting time of all customers is significantly more than 3 minutes, at 0.05 significant level
Explanation:
Step 1: State the hypothesis and identify the claim.
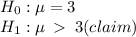
Step 2: We calculate the critical value. Since we were not given any significant level, we assume
 , and since this is a right tailed test, the critical value is z=1.65
, and since this is a right tailed test, the critical value is z=1.65
Step 3: Calculate the test statistic.
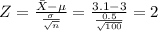
Step 4:Decide. Since the test statistic , 2 s greater than the critical value, 1.65, and it is in the critical region, the decision is to reject the null hypothesis.
Step 5: Conclusion, there is enough evidence to support the claim that the mean is greater than 3