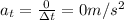Question

A spaceship negotiates a circular turn of radius 2925 km at a speed of 29960 km/h. (a) What is the magnitude of the angular speed? 0.0028 Correct: Your answer is correct. rad/s (b) What is the magnitude of the radial acceleration? 23.68 Correct: Your answer is correct. m/s2 (c) What is the magnitude of the tangential acceleration? m/s2

Answer 1

a) 0.0028 rad/s

b)
`23.68 m/s^2`

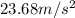
c)
`0 m/s^2`

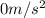
Step-by-step explanation:

a)

When an object is in circular motion, the angular speed of the object is the rate of change of its angular position. In formula, it is given by

`\omega = (\theta)/(t)`

where

`\theta` is the angular displacement

t is the time interval

The angular speed of an object in circular motion can also be written as

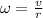`\omega = (v)/(r)` (1)

where

v is the linear speed of the object

r is the radius of the orbit

For the spaceship in this problem we have:

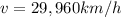`v=29,960 km/h` is the linear speed, converted into m/s,

`v=8322 m/s`

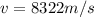
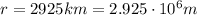`r=2925 km = 2.925\cdot 10^6 m` is the radius of the orbit

Subsituting into eq(1), we find the angular speed of the spaceship:

`\omega=(8322)/(2.925\cdot 10^6)=0.0028 rad/s`

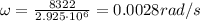
b)

When an object is in circular motion, its direction is constantly changing, therefore the object is accelerating; in particular, there is a component of the acceleration acting towards the centre of the orbit: this is called centripetal acceleration, or radial acceleration.

The magnitude of the radial acceleration is given by

`a_r=\omega^2 r`

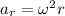
where

`\omega` is the angular speed

`r` is the radius of the orbit

For the spaceship in the problem, we have

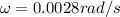`\omega=0.0028 rad/s` is the angular speed

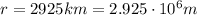`r=2925 km = 2.925\cdot 10^6 m` is the radius of the orbit

Substittuing into the equation above, we find the radial acceleration:

`a_r=(0.0028)^2(2.925\cdot 10^6)=23.68 m/s^2`

c)

When an object is in circular motion, it can also have a component of the acceleration in the direction tangential to its motion: this component is called tangential acceleration.

The tangential acceleration is given by

`a_t=(\Delta v)/(\Delta t)`

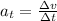
where

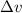`\Delta v` is the change in the linear speed

`\Delta t` is the time interval

In this problem, the spaceship is moving with constant linear speed equal to

`v=8322 m/s`

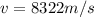
Therefore, its linear speed is not changing, so the change in linear speed is zero:

`\Delta v=0`

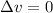
And therefore, the tangential acceleration is zero as well:

`a_t=(0)/(\Delta t)=0 m/s^2`