Question

The figure is made up of a cylinder and a sphere which has been cut in half. The radius of each half sphere is 5 mm. What is

the volume of the composite figure? Use 3.14 for Round to the nearest hundredth.
5 mm
10 mm
Recall the formulas y-Bhand V-
376.80 cubic millimeters
847 80 cubic millimeters
1.177 50 cubic millimeters
1308 33 cubic millimeters

Answer 1

Rounded to the nearest hundredth the volume of the composite figure is:

1308 33 cubic millimeters

Step-by-step explanation:

Hello! I wrote the complete question in a comment above. The volume of a cylinder is defined as:

`V_(c)=\pi r^2 h \\ \\ r:radius \\ \\ h:height`

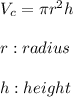
While the volume of half a sphere is:

`V_(hs)=(2)/(3)\pi r^3`

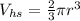
Since we have 2 half spheres, then the volume of these is the same as the volume of a sphere:

`V_(s)=(4)/(3)\pi r^3`

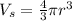
Then, the composite figure is:

`V=\pi r^2 h +(4)/(3)\pi r^3 \\ \\ V=\pi r^2(h+(4)/(3)r)`

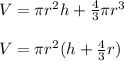
The radius of the cylinder is the same of the radius of each half sphere. So:

`r=5mm \\ \\ h=10mm \\ \\ \\ V=(3.14) (5)^2((10)+(4)/(3)(5)) \\ \\ V=25(3.14)(10+(20)/(3)) \\ \\ \boxed{V\approx 1308.33mm^3}`