Answer:
(2,45) ; x = 2
Explanation:
The method for solving for the vertex of a parabola from standard form involves converting to vertex form by forming a squared term. First, we need to actually put this equation into standard form, which dictates that the x^2 must never have a number in front of it (including -1). This means factoring out a negative 5 from the whole left side:
-5 (x^2 - 4x - 5) = y.
The next step is to pull the -5 out of the parentheses,
-5 (x^2 - 4x) + 25 = y,
which means multiplying it by the term on the outside to result in a positive 25. From here, we form the squardo term from what is inside the parentheses. We do this by changing the form of the equation, similar to how one changes the form of a fraction (multiplying by a number over the same number so that you are effectively multiplying by one). Inside of the parentheses, we a going to add a number and on the outside of the parentheses, we are going to subtract that number multiplied by what is in front of the parentheses (effectively adding zero to the equation):
-5 (x^2 - 4x + __) +25 - (-5*__) = y.
Now, the number that goes in the blank is the coefficient of the x divided by two and then squared:
__= (-4/2)^2,
__= 4.
From there, we just plug in the __ , simplify, and factor:
-5 (x^2 - 4x + (4)) + 25 - (-5*(4)) = y,
-5 (x^2 - 4x + 4) + 25 - (-20) = y,
-5 (x^2 - 4x + 4) + 45 = y,
-5 (x - 2) (x - 2) + 45 = y,
-5 (x - 2)^2 + 45 = y.
Now the equation is in vertex form, and from it, we can determe the vertex. The general equation for vertex form is
m (x -
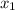 ) +
) +
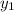 = y,
= y,
where (
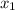 ,
,
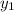 ) is the vertex. *Notice that there is a negative sign built in to the equation, so when you pull out
) is the vertex. *Notice that there is a negative sign built in to the equation, so when you pull out
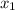 , make sure that you leave behind a negative sign. In our case, we pull out a positive two, leaving behind the negative sign. *If it were a ( x + 2 ), we would change it into ( x - (-2)) and pull out the -2, leaving behind a negative sign.*
, make sure that you leave behind a negative sign. In our case, we pull out a positive two, leaving behind the negative sign. *If it were a ( x + 2 ), we would change it into ( x - (-2)) and pull out the -2, leaving behind a negative sign.*
This gives us a vertex of (2,45).
Now, the second part of the question asks for the equation of the axis of symmetry. The general equation for the axis of symmetry is
x =
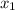 ,
,
since the axis of symmetry is just a vertical line that goes through the vertex. Plugging in
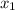 then gives us
then gives us
x = 2,
our axis of symmetry.