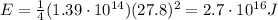Question

Hurricanes can involve winds in excess of 100 km/h at the outer edge. Make a crude estimate of the energy of such a hurricane, approximating it as a rigidly rotating uniform cylinder of air (density 1.3 kg/m3) of radius 88 km and height 4.4 km .

Answer 1

`2.7\cdot 10^(16) J`

Step-by-step explanation:

We can approximate the hurricane as a rotating uniform cylinder, so its energy is the rotational kinetic energy, given by:

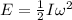`E=(1)/(2)I\omega^2` (1)

where

I is the moment of inertia

`\omega` is the angular velocity

The moment of inertia of a cylinder rotating about its axis is

`I=(1)/(2)MR^2`

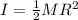
where

M is the mass

R is the radius

So formula (1) can be written as

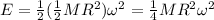`E=(1)/(2)((1)/(2)MR^2)\omega^2=(1)/(4)MR^2\omega^2` (2)

For an object in rotation, the linear speed at the edge is related to the angular velocity by

`v=\omega R`

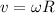
So we can rewrite (2) as

`E=(1)/(4)Mv^2`

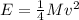
where we have:

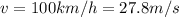`v=100 km/h = 27.8 m/s` is the speed at the edge of the hurricane

We have to calculate the mass of the cylinder. We have:

`R=88 km = 88,000 m` (radius)

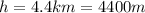`h=4.4 km = 4400 m` (height)

So the volume is

`V=\pi R^2 h = \pi (88,000)^2 (4400)=1.07\cdot 10^(14) m^3`

The density is

`\rho = 1.3 kg/m^3`

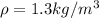
So the mass is

`M=\rho V=(1.3)(1.07\cdot 10^(14))=1.39\cdot 10^(14) kg`

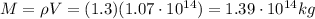
Therefore, the energy is

`E=(1)/(4)(1.39\cdot 10^(14))(27.8)^2=2.7\cdot 10^(16) J`