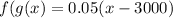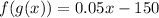Answer:
1.
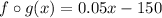
2.

3. The first one represents Dale's commission
Step-by-step explanation:
1. The composition of the function
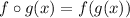
means that you first apply the function g(x) and then f(x) on the output of g(x).
That is:
- f(x) = 0.05x
- g(x) = x - 3000
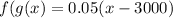
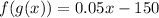
2. The composition of the function

means that you first apply the function f(x) and then g(x) on the output of f(x).
That is:
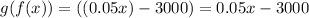
3. Which one represents Dale's commission
To calculate Dales's commision you must subtract $3,000 from the sales, to find the sales over $3000. That is: x - 3,000, which is the function g(x).
Therefore, you first use g(x).
Then, you must multiply the output of g(x) by 0.05 to find the 5% of the sales over $3,000. That is: 0.05(g((x)) = 0.05(x - 3000) = 0.05x - 150.
Therefore, the composition that represents Dale's commission is the first one: