Question

Suppose ACT Reading scores are normally distributed with a mean of 21.3 and a standard deviation of 5.9. A university plans to award scholarships to students whose scores are in the top 7%. What is the minimum score required for the scholarship? Round your answer to the nearest tenth, if necessary.

Answer 1

30.0

Explanation:

Given our data is normally distribute with
`\mu=21.3` and
`\sigma=5.9`

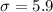
-Top 7% is given by find the z-value corresponding to p=(1-0.07)=0.93

-We substitute our values in the equation below;

`z=(\bar X-\mu)/(\sigma)\\\\\\=(X-21.3)/(5.9), z_(0.035)=1.476\\\\\therefore 1.476=(X-21.3)/(5.9)\\\\X=5.9* 1.476+21.3\\\\=30.0084\approx30.0`

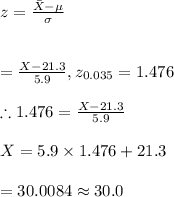
Hence, the minimum score required for the scholarship is 30.0