Question

It has been estimated that only about 30% of California residents have adequate earthquake supplies. Suppose you randomly survey 11 California residents. We are interested in the number who have adequate earthquake supplies.What is the probability that at least 8 have adequate earthquake supplies?

Is it more likely that none or that all of the residents surveyed will have adequate earthquake
supplies? Why?

Answer 1

`P(X\geq 8)=0.0043\\\\`

It's more likely that all of the residents surveyed will have adequate earthquake supplies since it has a probability of 98.02% which is very close to 100%.

Explanation:

-This is a binomial probability problem with the function:

`P(X=x)={n\choose x}p^x(1-p)^(n-x)`

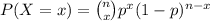
-Given p=0.3, n=11, the is calculated as:

`P(X=x)={n\choose x}p^x(1-p)^(n-x)\\\\P(X\geq 8)=P(X=8)+P(X=9)+P(X=10)+P(X=11)\\\\={11\choose 8}0.3^8(0.7)^3+{11\choose 9}0.3^9(0.7)^2+{11\choose 10}0.3^(10)(0.7)^1+{11\choose 11}0.3^(11)(0.7)^0\\\\=0.0037+0.0005+0.00005+0.000002\\\\=0.0043`

Hence, the probability that at least 8 have adequate supplies 0.0043

#The probability that non has adequate supplies is calculated as;

`P(X=x)={n\choose x}p^x(1-p)^(n-x)\\\\P(X= 0)={11\choose 0}0.3^(0)(0.7)^(11)\\\\=0.0198`

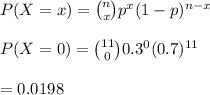
#The probability that all have adequate supplies is calculated as:

`P(X=x)={n\choose x}p^x(1-p)^(n-x)\\\\P(X= All)=1-{11\choose 0}0.3^(0)(0.7)^(11)\\\\=1-0.0198\\\\=0.9802`

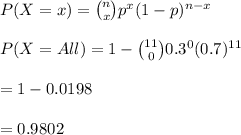
Hence, it's more likely that all of the residents surveyed will have adequate earthquake supplies since
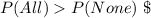`P(All)>P(None)\ \` and that this probability is 0.9802 or 98.02% a figure close to 1