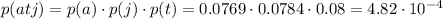Question

Three cards are drawn from a standard deck of 52 cards without replacement. Find the probability that the first card is an ace, the second card is a three, and the third card is a jack.

Answer 1

`4.82\cdot 10^(-4)`

Explanation:

In a deck of cart, we have:

a = 4 (aces)

t = 4 (three)

j = 4 (jacks)

And the total number of cards in the deck is

n = 52

So, the probability of drawing an ace as first cart is:

`p(a)=(a)/(n)=(4)/(52)=(1)/(13)=0.0769`

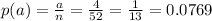
At the second drawing, the ace is not replaced within the deck. So the number of cards left in the deck is

`n-1=51`

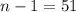
Therefore, the probability of drawing a three at the 2nd draw is

`p(t)=(t)/(n-1)=(4)/(51)=0.0784`

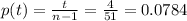
Then, at the third draw, the previous 2 cards are not replaced, so there are now

`n-2=50`

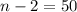
cards in the deck. So, the probability of drawing a jack is

`p(j)=(j)/(n-2)=(4)/(50)=0.08`

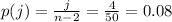
Therefore, the total probability of drawing an ace, a three and then a jack is:

`p(atj)=p(a)\cdot p(j) \cdot p(t)=0.0769\cdot 0.0784 \cdot 0.08 =4.82\cdot 10^(-4)`