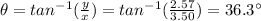Answer:
4.34 mi at
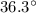 north of east
north of east
Step-by-step explanation:
The displacement of an object in motion is a vector connecting its initial position to the final position of motion.
In this problem, the man has 2 different motions:
- 3.50 mi due east
- 2.57 mi due north
We can take the east direction as positive x-direction and north as positive y-direction, so these two motions can be written as:
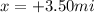
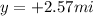
Since the two motions are perpendicular to each other, the resultant displacement can be found by using Pythagorean's theorem; therefore:
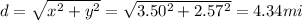
We can also find the direction using the equation:
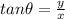
And therefore,