Answer:
The z-score for SAT exam of junior is much small than his ACT score. This means he performed well in his ACT exam and performed poor in his SAT exam.
Explanation:
Mean SAT scores = 1026
Standard Deviation = 209
Mean ACT score = 20.8
Standard Deviation = 4.8
We are given SAT and ACT scores of a student and we have to compare them. We cannot compare them directly so we have to Normalize them i.e. convert them into such a form that we can compare the numbers in a meaningful manner. The best way out is to convert both the values into their equivalent z-scores and then do the comparison. Comparison of equivalent z-scores will tell us which score is higher and which is lower.
The formula to calculate the z-score is:

Here, μ is the mean and σ is the standard deviation. x is the value we want to convert to z score.
z-score for junior scoring 860 in SAT exam will be:
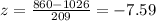
z-score for junior scoring 16 in ACT exam will be:
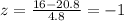
The z-score for SAT exam of junior is much small than his ACT score. This means he performed well in his ACT exam and performed poor in his SAT exam.