Answer:
The velocity of the composite body is 0.99m/s 63.43° west of north.
Step-by-step explanation:
Here the law of conservation of energy says that
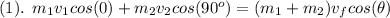
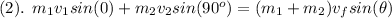
where
 is the final velocity if the composite body, and
is the final velocity if the composite body, and
 is measured from west of north.
is measured from west of north.
Putting in numbers and simplifying the above equation we get:

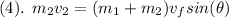
dividing equation (4) by (3) gives
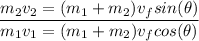
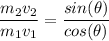
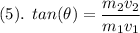
putting in
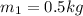 ,
,
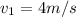 ,
,
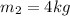 , and
, and
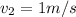 we get:
we get:
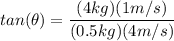
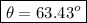
Thus, the final velocity
 we get from equation (3) is:
we get from equation (3) is:
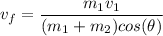
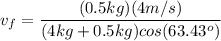

Thus, the velocity of the composite body is 0.99m/s 63.43° west of north.