Question

Find the length of RS.

Answer 1

Given:

The length of arc TS = 40 in

To find:

The length of arc RS.

Solution:

Length of TS = 40 in

θ = 80°

Using arc length formula:

`$\text { Arc length }=2 \pi {r}\left((\theta)/(360)\right)`

`$40=2 * 3.14 * {r}\left((80)/(360)\right)`

`$40=6.28 * {r}\left((2)/(9)\right)`

`$40=1.39* r`

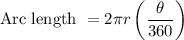
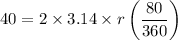
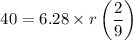
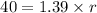
Divide by 1.39 on both sides, we get

`28.7=r`

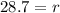
Radius = 28.7

Complete angle of circle = 360°

Angle measure of RS = 360° - 60° - 120° - 80°

Angle measure of RS = 100°

Arc length of RS:

`$\text { Arc length }=2 \pi {r}\left((\theta)/(360)\right)`

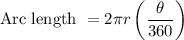
Substitute θ = 100° and r = 28.7

`$=2 * 3.14 * 28.7 \left((100)/(360)\right)`

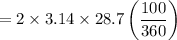
= 50 inch

The length of arc Rs is 50 inches.