Question

Suppose 40% of DC area adults have traveled outside of the United States. Nardole wants to know if his customers are atypical in this respect. He surveys 40 customers and finds 60% have traveled outside of the U.S. Is this result a statistically significant difference?

Answer 1

We conclude that % of DC area adults who have traveled outside of the United States is different from 40%.

Explanation:

We are given that 40% of DC area adults have traveled outside of the United States. Nardole wants to know if his customers are typical in this respect. He surveys 40 customers and finds 60% have traveled outside of the U.S.

We have to test is this result a statistically significant difference.

Let p = % of DC area adults who have traveled outside of the United States

SO, Null Hypothesis,
`H_0` : p = 40% {means that 40% of DC area adults have traveled outside of the United States}

Alternate Hypothesis,
`H_a` : p
`\\eq` 40% {means that % of DC area adults who have traveled outside of the United States is different from 40%}

The test statistics that will be used here is One-sample z proportion statistics;

T.S. =
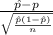`\frac{\hat p-p}{\sqrt{(\hat p(1- \hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = % of customers who have traveled outside of the United States

in a survey of 40 customers = 60%

n = sample of customers = 40

So, test statistics =
`\frac{0.60-0.40}{\sqrt{(0.60(1-0.60))/(40) } }`

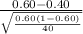
= 2.582

Since in the question we are not given with the significance level so we assume it to be 5%. So, at 0.05 level of significance, the z table gives critical value of 1.96 for two-tailed test. Since our test statistics is more than the critical value of z so we have sufficient evidence to reject null hypothesis as it will fall in the rejection region.

Therefore, we conclude that % of DC area adults who have traveled outside of the United States is different from 40%.